2.1 Trazos de lineas rectas
Las
líneas en OpenGL son en realidad segmentos acotados, en lugar de la
idea matemática de rectas infinitas. Su definición viene dada por la
especificación del valor de sus dos vértices extremos.
Consideremos
una línea recta que pasa por dos puntos P1=[20, 20] y [25,20]. Podemos
calcular la línea recta que pasa por estos puntos como
(y-y1) = (y2-y1)*(x-x1)/(x2-x1)
Sustituyendo los valores tenemos
(y-20) = (21-20)*(x-20)/(25-20)
Finalmente tenemos
y = 0.2 x + 16
Podemos calcular los valores utilizando el siguiente código
void linea(int x0, int y0, int x1, int y1)
{ int x;
float dy, dx, y, m;
dy = y1 - y0;
dx = x1 - x0;
m = dy/dx;
y = y0;
for(x = x0; x <= x1; x++)
{ escribir_pixel(x, (int) floor(y+0.5) );
y +=m; } }
Note que se suma 0.5 y se calcula la parte entera para redondear la solución.
2.2 Representación y trazo de poligonos
OpenGL
maneja polígonos correctamente siempre y cuando sean simples y
convexos. Si ese no es el caso, OpenGL dibuja cosas raras.
Además
en algunas ocasiones se quiere especificar el vector normal del plano
en el cual se encuentra el polígono. Dicho vector normal se necesita
p.e. para algoritmos de visualización avanzada (``Phong shading'').
Cuando
se escriben aplicaciones gráficas nos enfrentamos con el problema
siguiente: desde alguna fuente ``vienen'' listas de puntos (o bien de
otro programa, o bien de un fichero, o bien de modo interactivo) y hay
que interpretar las listas como polígonos, es decir, hay que verificar
si las listas cumplen la definición de especificar polígonos simples y
convexos. Si ese no es el caso, a lo mejor se pueden ``corregir'' las
listas. (Programas con tal propiedades se llama robustos y tolerantes.)
Entonces (en el caso de mera visualización con OpenGL):
Se puede eliminar puntos múltiples consecutivos en la lista.
Se puede intentar calcular el plano en el cual se encuentran más o menos los puntos del polígono (eso no es tan trivial).
En
dicho plano, es decir, una vez corregidos los puntos hasta que se
encuentren exactamente en el plano, se puede verificar si el polígono es
simple y convexo (eso es algo bastante fácil).
Si
no es así, se podría subdividir el polígono en partes simples y
convexos para seguir trabajando después con las partes sin problemas
(este paso no lo vamos a realizar en estas prácticas).
Antes de dedicarnos a los detalles, dibujamos polígonos con OpenGL asumiendo que la lista de puntos cumple la definición.
Siempre
que se quiera dibujar un objeto de OpenGL (en este caso unos polígonos,
antes vimos puntos y segmentos), hay que decírselo de antemano con la
función
glBegin()
La lista de puntos se define con consecutivas llamadas a
glVertex*()
y se termina el trabajo con
glEnd()
En
lugar de dibujar polígonos rellenados, OpenGL puede dibujar, o bien
solo las esquinas o bien solo los segmentos del borde. Eso se realiza
con la función
glPolygonMode()
a la cual hay que pasar también cuál de las dos posibles caras del polígono se quiere pintar.
Además se pueden llenar los polígonos con patrones que no detallamos por el momento.
glEnable()
glPolygonStipple()
ALGORITMO DE BRESENHAM PARA TRAZAR LÍNEAS
El algoritmo de Bresenham es un algoritmo que determina los puntos en un mapa de bits de n dimensiones que deben ser trazados con el fin de formar una aproximación a una línea recta entre dos puntos dados.
Es comúnmente usado para dibujar líneas en una pantalla de ordenador, ya que utiliza sólo adición de enteros, la resta y desplazamiento de bits, que son operaciones muy barato en las arquitecturas de ordenador estándar. Es uno de los primeros algoritmos desarrollados en el campo de gráficos por ordenador. Una extensión menor a la del algoritmo original también se ocupa de dibujar círculos.
ALGORITMO DE BRESENHAM PARA TRAZAR CIRCUNFERENCIAS
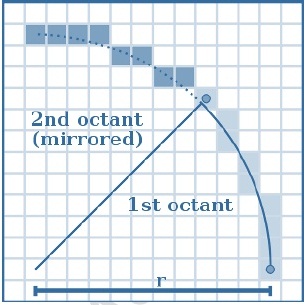
En graficación, el algoritmo de “mid point circle” es un algoritmo utilizado para determinar los puntos necesarios para dibujar un círculo.
El algoritmo es una variante del algoritmo de la línea Bresenham, por lo que es a veces conocido como algoritmo de círculo Bresenham, aunque en realidad no inventada por Bresenham. El algoritmo comienza en consecuencia con el círculo de la ecuación
x2+y 2=r2.
Así, el centro del círculo se encuentra en (0,0). Consideramos que sólo la primera el octante primera y trazar una curva que comienza en el punto (r,0) y hacia arriba los ingresos ya la izquierda, llegando al ángulo de 45 °. La dirección “rápida” aquí es la dirección vertical. El algoritmo hace siempre un paso en la dirección positiva (hacia arriba), y de vez en cuando también tiene que hacer un paso en la "lenta" la dirección, la dirección x negativa. De la ecuación de un círculo se obtiene la ecuación transformada
x2+y 2-r2= 0, donde r2 se calcula sólo una sola vez durante la inicialización
2.3 Transformaciones bidimensionales
Con los procedimientos para desplegar primitivos de salida y sus atributos, podemos crear
una variedad de imágenes y gráficas. En muchas aplicaciones también es necesario alteraro ma-
nipular los despliegues. Se crean aplicaciones de diseño y planos de construcciones al ordenar las orientaciones y los tamaños de las partes que componen la escena. Las transformaciones geométricas básicas son traslación, rotación y escalación. Otras transformaciones que se aplican con frecuencia en objetos incluyen la reflexión y el recorte. Primero analizamos los métodos para realizar transformaciones geométricas.
Translacion
Se aplica una traslación en un objeto para cambiar su posición a lo largo de la trayectoria de una línea recta de una dirección de coordenadas a otra. Convertimos un punto bidimensional al agregar las distancias de traslación, tx y ty la posición de coordenadas original (x,y)
El par de distancia de traslación se llama vector de traslación o vector de cambio. Se pueden expresar las ecuaciones anteriores en una sola ecuación matricial al utilizar vectores de columna para representar las posiciones de coordenadas y el vector de traslación
Los polígonos se trasladan al sumar el vector de traslación a la posición decoordenadas de cada vértice y se vuelve a generar el polígono utilizando un nuevo conjuntode coordenadas y vértices y las especificaciones actuales de los atributos.

Rotación
Se aplica una rotación bidimensional en un objeto al cambiar su posición a lo largo de la trayectoria de una circunferencia en el plano de xy . Para generar una rotación, especificamos un ángulo de rotación θ y la posición (x r , y r ) del punto de rotación (o punto pivote) en torno al cual se gira el objeto.

Escalación
Una transformación de escalación altera el tamaño de un objeto. Se puede realizar esta operación para polígonos al multiplicar los valores de coordenadas (x, y) de cada vértice por los factores de escalación s x y s y para producir las coordenadas transformadas (x’, y’ ).
2.4 Representación matricial
El primer renglón nos dará el número complejo. Podemos definir la unidad real como
y la imaginaria como
al ser un número complejo la suma de un número real más otro número real por la unidad imaginaria, podemos hacerlo matricialmene
Con esta representación la aritmetica compleja es isomorfa a las operaciones con matrices.
2.5 Ventana y puerto de visión
Definicion.
El puerto de vision es el area de la ventana grafica en la que se colocan las fotografias de la camara virtual. Normalmente el puerto de vision coincide con toda el area de la ventana grafica, pero es posible tener varios puertos de vison en una sola ventana.
COLOCACIÓN DE VENTANAS Y RECORTE
Los programas de aplicaciones definen imágenes en un sistema de coordenadas mundiales. Este puede ser cualquier sistema de coordenadas Cartesianas que un usuario halle conveniente. Las imágenes definidas en coordenadas mundiales son procesadas por el sistema de graficas en coordenadas de dispositivo. Comúnmente, un paquete de graficas permite a un usuario especificar qué área de la definición de la imagen se desplegara y donde se colocara en el dispositivo de despliegue. Podría elegirse una sola área para el dispositivo de despliegue o bien podrían seleccionarse varias áreas. Estas áreas pueden colocarse en localidades aparte del despliegue o bien un área puede servir como una pequeña inserción en un área mayor. Este proceso de transformación implica operaciones para trasladar y escalar áreas seleccionadas y para borrar partes de la imagen que estén fuera de las áreas. Estas operaciones se conocen como colocación de ventanas y recorte.
CONCEPTOS DE COLOCACIÓN DE VENTANAS
Un área rectangular que se especifica en coordenadas mundiales se denomina ventana. El área rectangular en el dispositivo de despliegue en el cual se coloca la ventana se llama puerta de visión. La figura 1 ilustra el trazo o planimetría de la selección de una imagen que queda dentro del área de ventana en una puerta de visión designada. Esta planimetría se llama transformación de la visión o bien transformación de normalización.

Fuente:
- http://julian09110907.blogspot.mx/2012/02/graficacion-2d.html
- http://www.sistemas.edu.bo/cbalderrama/sis%201201/LIBRO/tema%203.pdf
- http://fernandez-torres-jose.blogspot.mx/2012/09/21-transformaciones-bidimensionales.html
- http://delta.cs.cinvestav.mx/~mcintosh/comun/summer2006/complexJulio_html/node7.html
- http://garciaoscar10110795.blogspot.mx/p/unidad-iii.html
- http://graficacionitca3d.blogspot.mx/2012/03/24-transformacion-ventana-area-de-vista.html